Discussion Forum



1)

 Two ideal batteries of emf V1  and V2    and three resistance R1, R2  and R3 are connected as shown in the figure. The current in resistance  R2 would be zero if

2132021553_resis.JPG

 


A) $V_{1}=V_{2}$ and $R_{1}=R_{2}=R_{3}$

B) $V_{1}=V_{2}$ and $R_{1}=2R_{2}=R_{3}$

C) $V_{1}=2V_{2}$ and $2R_{1}=2R_{2}=R_{3}$

D) $2V_{1}=V_{2}$ and $2R_{1}=R_{2}=R_{3}$

Answer:

Option A,B,D

Explanation:

Let us take  $V_{P}=0$  .Then potentials  acrosds  $R_{1}$, $R_{2}$   and $R_{3}$ are as shown in figure(ii)

In the same figure.

 2132021220_same.JPG

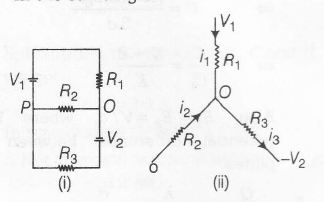
      i1 +i2  =i3

$\therefore$    $ \frac{V_{1}-V_{0}}{R_{1}}+\frac{0-V_{0}}{R_{2}}=\frac{V_{0}-(-V_{2})}{R_{3}}$

 Solving this equation  we get,

 $V_{0}=\frac{\frac{V_{1}}{R_{1}}+0-\frac{V_{2}}{R_{2}}}{\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}}$

  Current througfh R2 will be zero if

$V_{0}=0\Rightarrow\frac{V_{1}}{V_{2}}=\frac{R_{1}}{R_{2}}$

 In options (a),(b), and (d)  this reaction is satisfied