Discussion Forum



1)

 In the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle θ with the horizontal floor. The coefficient of frictional between the wall and ladder is  $ \mu_{1}$  and that between the floor and the ladder is  $\mu_{2}$. The normal reaction of the wall on the ladder is N1 and that of the floor is N2. If the ladder is about to slip, then

2132021606_cap.JPG


A) $\mu_{1}=0,\mu_{2}\neq0 $ and $N_{2}\tan\theta=\frac{mg}{2}$

B) $\mu_{1}\neq 0,\mu_{2}=0 $ and $N_{1}\tan\theta=\frac{mg}{2}$

C) $\mu_{1}\neq 0,\mu_{2}\neq0$ and $N_{2}=\frac{mg}{1+\mu_{1}\mu_{2}}$

D) $\mu_{1}= 0,\mu_{2}\neq0$ and $N_{1}\tan\theta=\frac{mg}{2}$

Answer:

Option C,D

Explanation:

$ \mu_{2}$ can never be zero for maximum equilibrium.

2132021701_eq.JPG

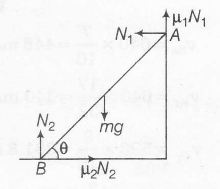
when  $\mu_{1}$ = 0 we have

  $N_{1}=\mu_{2}N_{2}$    ..........(i)

     $N_{1}=m_{2}g$       ...........(ii)

$\tau_{B}=0\Rightarrow mg\frac{L}{2}\cos\theta=N_{1}L\sin\theta$

$\Rightarrow $   $N_{1}=\frac{mg \cot \theta}{2}$

$\Rightarrow$    $ N_{1}\tan \theta=\frac{mg }{2}$

 when  $\mu_{1}\neq 0$ we have

 $\mu_{1}N_{1}+N_{2}=mg$      ........(i)

  $\mu_{2}N_{2}$= N        .......(ii)

 $\Rightarrow$      $ N_{2}=\frac{mg}{1+\mu_{1}\mu_{2}}$