Discussion Forum



1)

At time t=0 terminal A in the circuit shown in the figure is connected to B by a key and an alternating current I(t)= I0 $\cos (\omega t) $ with I0 =I A and $\omega $= 500 rad s-1 starts flowing in it with the initial direction shown in the figure. At t= $\frac{7\pi}{6\omega}$, the key is switched from B to D. Now onwards only A and D are connected. A total charge Q flows from the battery to charge the capacitor fully. If C= 20μ F, R=10Ω and the battery is ideal with emf of 50 V, identify the correct statement (s)


A) Magnitude of the maximum charge in the capacitor before $t= \frac{7\pi}{6\omega}$ is $1\times 10^{-3}C$

B) The current in the left part of the circuit just before $t= \frac{7\pi}{6\omega} $ is clock wise

C) Immediately after A is connected to D, the current Is R is 10 A

D) $Q= 2\times 10^{-3} C$

Answer:

Option C,D

Explanation:

$\frac{dQ}{dt}=I\Rightarrow Q=\int_{}^{} I dt=\int_{}^{} (I_{0}\cos \omega t)dt$

 $\therefore $        $ Q_{max}=\frac{I_{0}}{\omega}=\frac{1}{500}=2 \times 10^{-3}C$

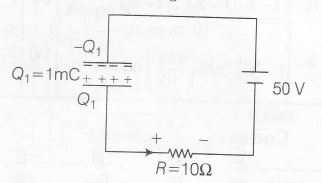
  Justrt after switching

2132021293_switching.JPG

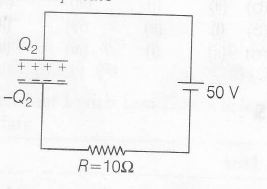
 In steady state,

 2132021695_steady.JPG

At     $t=\frac{7\pi}{6\omega}$    or    $\omega t=\frac{7\pi}{6} $

   Current comes out to be negative from the given expression. So , current is anti-clockwise.

  Charge supplied by source from t=0 to t =  $\frac{7\pi}{6\omega}$

  $Q=\int_{0}^{\frac{7\pi}{6\omega}}  \cos (500t) dt$

    $=\left[\frac{\sin 500t}{500}\right]^{\frac{7\pi}{6\omega}}_{0}=\frac{\sin \frac{7\pi}{6}}{500}=-1mC$

  Apply Kirchhoff's loop law  just after changing the switch to position D

    $ 50+\frac{Q_{1}}{C}-IR=0$

substituting  the values of Q1 , C and R we get,

   I= 10A

   In steady state Q2= CV=1mC

 $\therefore$    Net charge flown from battery= 2mC