Answer:
Option A
Explanation:
Given curves are $y=\sqrt{x}$ ........(i)
and 2y-x+3=0 .......(ii)
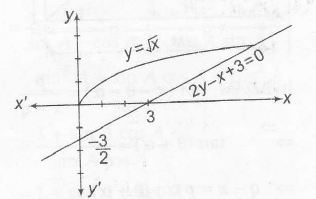
On solving Eqs(i) and (ii) , we get
$2\sqrt{x}-(\sqrt{x})^{2}+3=0$
$\Rightarrow$ $(\sqrt{x})^{2}-2\sqrt{x}-3=0$
$\Rightarrow$ $(\sqrt{x}-3)(\sqrt{x}+1)=0$
$\Rightarrow$ $\sqrt{x}=3$
( $\therefore$ $\sqrt{x}=-1 $ is not possible)
$\therefore$ y=3
$\therefore$ Required area = $\int_{0}^{3} (x_{2}-x_{1})dy$
$\int_{0}^{3} ((2y+3)-y^{2})dy$
= $\left[y^{2}+3y-\frac{y^{3}}{3}\right]_{0}^{3}$
=9+9-9=9