Discussion Forum



1)

A uniform cylinder of length l and mass M having cross-sectional area A is suspended, with its length vertical from a fixed point by a massless spring such that it is half-submerged in a liquid of density, σ  at the equilibrium position. The extension x0 of the spring when it is  in equilibrium is 


A) $\frac{Mg}{k}$

B) $\frac{Mg}{k}\left(1-\frac{LA_{0}}{M}\right)$

C) $\frac{Mg}{k}\left(1-\frac{LA_{0}}{2M}\right)$

D) $\frac{Mg}{k}\left(1+\frac{LA_{0}}{M}\right)$

Answer:

Option C

Explanation:

In equilibrium

 3032021790_p1.JPG

 

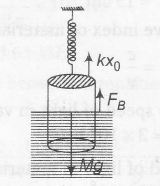
 Upward force= Downward force

$kx_{0}+F_{B}=mg$

 Here , kx0 is . restoring force of spring and FB is buoyancy force

$kx_{0}+\sigma\frac{L}{2}Ag=Mg$

$x_{0}=\frac{Mg-\frac{\sigma LAg}{2}}{k}$

$=\frac{Mg}{k}(1-\frac{\sigma LA}{2M})$