Discussion Forum

1)

A line L:y=mx+3 meets y-axis at E (0,3) and the arc of the parabola y²  =16 x ,  $0\leq y\leq6$ at the point F (x₀,y₀ ) . The tangent to the parabola at F (x₀,y₀) intersects the y axis at G(0,y₁). The slope m of the line L is chosen such that the area of the $\triangle$ EFG  has a local maximum

 Match List I with List II and select the correct answer using the code given below the lists

 

Answer:

Option A

Explanation:

Here,   $y^{2}=16x,0\leq y\leq6$

   

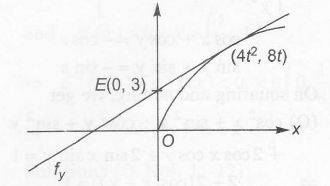
Tangent at F,

                   yt=x+at²

 at     x= 0, y= at=4t

 Also , (4t²,8t ) satisfy

   y=mx+c

 $\Rightarrow$    $ 8t=4mt^{2}+3$

$\Rightarrow $    $4mt^{2}-8t+3=0$

  $\therefore$   Area of $\triangle$  = $\frac{1}{2}\begin{bmatrix}0 & 3&1 \\0 &4t&1\\ 4t^{2}&8t&1 \end{bmatrix}=\frac{1}{2}4t^{2}(3-4t)$

A= 2[3t²-4t³]

 $\therefore$       $\frac{dA}{dt}=2[6t-12t^{2}]=-12t(2t-1)$

  

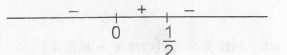
$\therefore$ Maximum at t=1/2

 and   $4mt^{2}-8t+3=0$

 $\Rightarrow$    m-4+3=0

 $\Rightarrow$   m=1

 G(0,4t)$\Rightarrow$  G(0,2)

y₁=2

 (x₀,y₀)  =(4 t²,8t)=(1,4)

 y₀=4

 Area   $=2\left(\frac{3}{4}-\frac{1}{2}\right)=\frac{1}{2}$