Answer:
Option B
Explanation:
Here, innermost function is inverse
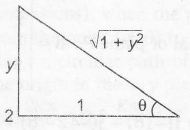
∴ put, tan−1y=θ⇒tanθ=y
⇒[1y2(cos(tan−1y)+ysin(tan−1y)cot−1(tan−1y)+tan(sin−1y))2+y4]1/2
⇒[1y2(1√1+y2+y2√1+y2√1−y2y+y√1−y2)2+y4]1/2
⇒[1y2.y2(1−y4)+y4]1/2=1
cos x +cos y= -cos z
sinx +sin y =-sinz
on squaring and adding , we get
(Q) cos2x+sin2x+cos2y+sin2y+2cosxcosy+2sinxsiny=1 ⇒ 2+2(cos(x−y)=1⇒ (cos(x−y)=−12 ⇒ 2cos2(x−y2)−1=−12⇒ 2cos2(x−y2)=12 ⇒cos(x−y2)=12 (R) cos2x(cos(π4−x)−cos(π4+x))+2sin2x=2sinxcosxcos2x(√2sinx)+2sin2x=2sinxcosx√2sinx(cos2x+√2sinx−√2cosx)=0 ⇒ sinx=0,(cosx−sinx)(cosx+sinx−√2)=0 ⇒ secx=1or1√2 (S) cot(sin−1√1−x2)=sin(tan−1(x√6)) ⇒ x√1−x2=x√6√1+6x2
= 12 x2 =5 x=√512=√52√3
P:4,Q:3,R:2,S:1