Discussion Forum

1)

Let  $S:S_{1}\cap S_{2} \cap S_{3}$ , where   

$S_{1}=\left\{ z\in C:|z|<4\right\}, S_{2}$ $=\left\{ z\in C :In\left[\frac{z-1+\sqrt{3}i}{1-\sqrt{3}i}\right]>0\right\}$

and   $S_{3}=\left\{ z\in C :Re z>0\right\}$

Area of S is equal to 

Answer:

Option B

Explanation:

 Here , $S=S_{1}\cap S_{2} \cap S_{3}$

 $S_{1}=\left\{ z\in C:|z|<4\right\}$

$\therefore$    S₁ :x²+y²   < 4   ...........(i)

 and   $S_{2}$ $=\left\{ z\in C :In\left[\frac{z-1+\sqrt{3}i}{1-\sqrt{3}i}\right]>0\right\}$

 where   $\frac{z-1+i\sqrt{3}}{1-i\sqrt{3}}= \frac{(x-1) +i(y+\sqrt{3})}{1-i\sqrt{3}}$

 =  $\frac{(x-1)(1+i\sqrt{3})+i(y+\sqrt{3}) (1+i\sqrt{3})}{1+3}$

 =$\frac{(x-1)+i\sqrt{3}(x-1)+i(y+\sqrt{3}) -\sqrt{3}(y+\sqrt{3})}{4}$

=$\frac{(x-1-\sqrt{3}y-3)}{4}+\frac{i(\sqrt{3}x+y)}{4}$

  $\therefore $     $s_{2}:\sqrt{3}x+y>0$  .......(ii)

  $S_{3}=\left\{ z\in C :Re z>0\right\}$

  $s_{3}:x>0$     ......(iii)

  $s_{3}:x>0$     ......(iii)

Since , 

                $S=S_{1}\cap S_{2} \cap S_{3}$

 

 

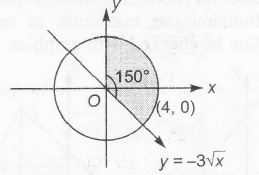
 Clearly , the shaded region represents the area of sector

 $\therefore$     $S= \frac{1}{2}r^{2}\theta=\frac{1}{2}\times 4^{2}\times\frac{5\pi}{6}=\frac{20\pi}{3}$