Discussion Forum

Let PQ be a focal chord of the parabola y²=4ax.The tangents to the parabola at P and Q meet at a point lying on the line y=2x+a, a >0

 If chord PQ subtends an angle $\theta$ at the vertex of y² =4ax, then tan $\theta$  is equal to 

Answer:

Explanation:

Concept involved

 Intersection point of tangents at  $(at_1^2,2at_{1})$ and $(at_2^2,2at_{2})$ is ( at₁t₂ , a/t₁ +t₂) ) , also tangents drawn  at end point of focal chord are perpendicular and intersect on directrix

$m_{op}=\frac{2at-0}{at^{2}-0}=\frac{2}{t}$

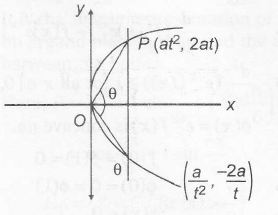
$m_{oQ}=\frac{-2a/t}{a/t^{2}}=-2t$

$\therefore$   $\tan\theta =\frac{\frac{2}{t}+2t}{1-\frac{2}{t}.2t}=\frac{2(t+\frac{1}{t})}{1-4}$

 where   ,   $t+\frac{1}{t}=\sqrt{5}=\frac{2\sqrt{5}}{-3}$