Answer:
Option B
Explanation:
Concept involved
Intersection point of tangents at (at21,2at1) and (at22,2at2) is ( at1t2 , a/t1 +t2) ) , also tangents drawn at end point of focal chord are perpendicular and intersect on directrix
Since R(−a,a(t−1t)) lies on y =2x+a
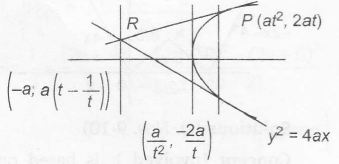
⇒ a.(t−1t)=−2a+a
⇒ t−1t=−1
Thus, length of focal chord
a(t+1t)2=a{(t−1t)2+4}=5a