Answer:
Option A,B
Explanation:
Concept involved
We know,
$|x|=\begin{cases}x & x \geq 0\\-x, & x < 0\end{cases}$
$\Rightarrow$ $ |x-a|=\begin{cases}x-a & x \geq0\\-(x-a) & x < a\end{cases}$
and for non-differentiable continuous function the maximum or minimum Can be checked with graph as
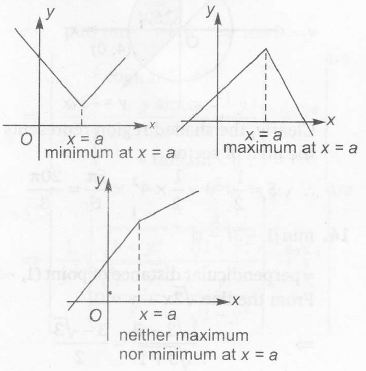
Here f(x) =2|x|+|x+2| -||x+2|-2|x||
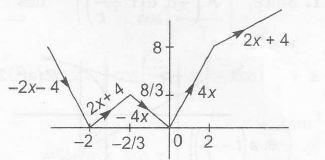
$=\begin{cases}-2x-(x+2)+(x+2), & when x\leq-2\\-2x+x+2+3x+2, & when -2<x\leq-2/3\\ -4x&when- \frac{2}{3}<x\leq0\\ 4x,&when 0<x\leq2\\ 2x+4,&when x>2\end{cases}$
$=\begin{cases}-2x-4, & x\leq-2\\2x+4, & -2<x\leq-2/3\\ -4x&- \frac{2}{3}<x\leq0\\ 4x,& 0<x\leq2\\ 2x+4,& x>2\end{cases}$
Graph for y=f(x) is shown as
