Answer:
Option C,D
Explanation:
Concept involved
It is simple representation of points on argand plane and to find the angle between the points
here, P=Wn=(cosπ6+isinπ6)n
=cosnπ6+isinnπ6
H1={Z∈C:Re(z)>12}
∴ P∩H1 represents those points for which cosnπ6 is +ve
∴ it belongs to I to IV quadrant
⇒ z1=P∩H1=cosπ6+isinπ6
or cos11π6+isin11π6
∴ z1=√32+i2or√32−i2 .....(i)
Similarly , z2=P∩H2 i,e. those points for which
cosnπ6<0
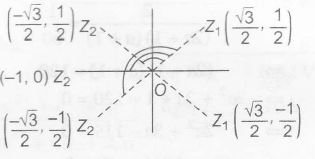
∴ z2=cosπ+isinπ,cos5π6
+isin5π6,cos7π6+isin7π6
⇒z2=−1,−√32+i2,−√32−i2
Thus, ∠z1Oz2=2π3,5π6,π