Discussion Forum

Circle (s) touching x-axis at a distance 3 from the origin and having an intercept of length  $2\sqrt{7}$ on the y-axis is (are)

Answer:

Explanation:

Concept involved

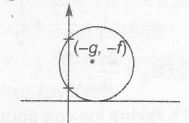
 Here, thr length of intercept on y-axis 

  $\Rightarrow$           $  2\sqrt{f^{2}-c}$

 and if circle touches x-axis

 $\Rightarrow$     $  g^{2}=c$

 for     $x^{2}+y^{2}+2gx+2fy+c=0$

 here, $x^{2}+y^{2}+2gx+2fy+c=0$

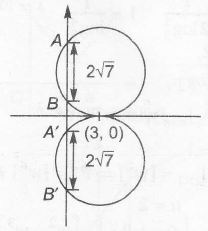
 Passes through (3,0)

 $\Rightarrow$        9+6g+c=0  ........(i)

    $g^{2}=c$    ..........(ii)

 and  $2\sqrt{f^{2}-c}=2\sqrt{7}$

          $f^{2}-c=7$     .........(iii)

 From Eqs .(i) and (ii), we get

 $g^{2}+6g+9=0$

    (g+3)²  =0

 g=-3

 and c=9  $\therefore$   f²=16

 $f=\pm 4$

 $\therefore$     $x^{2}+y^{2}-6x \pm 8y+9=0$