Discussion Forum

1)

 The radius of the orbit of an electron in a Hydrogen-like atom is 4.5 a₀ where a₀ is the Bohr radius. Its orbital angular moment is $\frac{3h}{2\pi}$. It is given that h is Planck constant and R is Rydberg constant. The possible  wavelength (s) when the atom de-excites,  is (are)

 

 

Answer:

Option A,C

Explanation:

$L=3(\frac{h}{2\pi})$

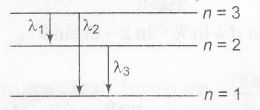
 $\therefore$   n=3 as  $L=3(\frac{h}{2\pi})$

    $r_{n}\propto\frac{n^{2}}{z}$

 r₃= 4.5 a₀  $\therefore$  z=2

$\frac{1}{\lambda_{1}}=Rz^{2}\left(\frac{1}{2^{2}}-\frac{1}{3^{2}}\right)=4R\left(\frac{1}{4}-\frac{1}{9}\right)$

$\therefore$   $\lambda_{1}=\frac{9}{5R}$

$\frac{1}{\lambda_{2}}=Rz^{2}\left(\frac{1}{1^{2}}-\frac{1}{3^{2}}\right)=4R\left(1-\frac{1}{9}\right)$

  $\Rightarrow$   $\lambda_{2}=\frac{9}{32R}$

$\frac{1}{\lambda_{3}}=Rz^{2}\left(\frac{1}{1^{2}}-\frac{1}{2^{2}}\right)=4R\left(1-\frac{1}{4}\right)$

$\Rightarrow$   $\lambda_{3}=\frac{1}{3R}$