Discussion Forum



1)

A  particle of mass m is attached to one end of the mass-less spring of force constant k, lying on a frictionless horizontal plane. The other end of the spring is fixed. The particle starts moving horizontally from its equilibrium position at time t=0 with an initial velocity $\mu_{0}$.When the speed of the particle is 0.5 $\mu_{0}$, it collides elastically with a rigid wall. After this collision


A) the speed of the particle when it returns to its equilibrium position is $\mu_{0}$

B) the time at which the particle passes through the equilibrium position for the first time is $t=\pi\sqrt{\frac{m}{k}}$

C) the time at hich the maximum compression of the spring occurs is $t=\frac{4\pi}{3}\sqrt{\frac{m}{k}}$

D) the time at which the particle passes through the equilibrium position for the second time is $t=\frac{5\pi}{3}\sqrt{\frac{m}{k}}$

Answer:

Option A,D

Explanation:

(a) At equilibrium (t=0)  particle has maximum velocity u0. Therefore  velocity at time t can be written as

1052021281_p2.JPG

 

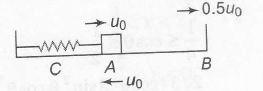
$u=u_{max}\cos \omega t+u_{0}\cos \omega t$

  writing, u=0.5 u0=u0 cos ω t

$\therefore$   $\omega t=\frac{\pi}{3}$

 $\therefore$    $\frac{2\pi}{T}t=\frac{\pi}{3}$   $\therefore$    $t=\frac{T}{6}$

 (b)     $t=t_{AB}+t_{BA}=\frac{T}{6}+\frac{T}{6}=\frac{T}{3}=\frac{2\pi}{3}\sqrt{\frac{m}{k}}$

  (c)     $t=t_{AB}+t_{BA}+t_{AC}=\frac{T}{6}+\frac{T}{6}+\frac{T}{4}=\frac{7}{12}T=\frac{7\pi}{6}\sqrt{\frac{m}{k}}$

 (d)   $t=t_{AB}+t_{BA}+t_{AC}+t_{CA}=\frac{T}{6}+\frac{T}{6}+\frac{T}{4}+\frac{T}{4}=\frac{5}{6}T=\frac{5\pi}{3}\sqrt{\frac{m}{k}}$