Discussion Forum

Consider the set of eight vectors  $V= [a\hat{i}+b\hat{j}+c \hat{k}:a,b,c\in\left\{-1,1\right\}] $ .Three non-coplannar vectors can be chosen from  V in 2^p ways. The , p is

Answer:

Explanation:

 Concept involved

 The three vectors are coplanar if volume is zero. Now, those vectors which are along the diagonals of a cube, are non-coplannar

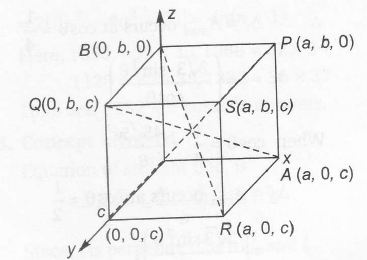
 Here, the four diagonals are

 OS, AQ, BR  and CP 

 Among set of eight vectors, four-vectors form body diagonals of a cube, imaging four will be parallel (unlike)  vectors.

 $\therefore$ Number of ways of selecting three vectors will be 

 $^{4}C_{3}\times 8=2^{5}=2^{p}$

         p=5