Answer:
Option A
Explanation:
Concept involved
As to maximise or minimise area of triangle we sholud find area is terms of parametric coordinate and we second derivative test.
Here , tangent at P(2cosθ,√3sinθ) is
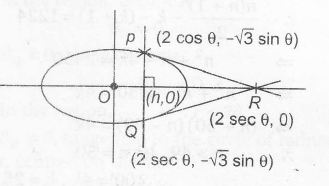
x2cosθ+y√3sinθ=1
∴ R(secθ,0)
⇒ △=areaof△PQR
=12(2√3sinθ)(2secθ−2cosθ)
=2√3.sin3θcosθ .........(i)
Since, 12≤h≤1,
∴ 12≤2cosθ≤1,
⇒ 14≤cosθ≤12
∴ d△dθ=2√3{cosθ.3sin3θcosθ−sin3θ(−sinθ)}cos2θ
= 2√3sin2θcos2θ[3cos2θ+sin2θ]
= 2√3sin2θcos2θ[2cos2θ+1]
= 2√3tan2θ(2cos2θ+1)>0
when, 14≤cosθ≤12
∴ △1=△max occurs at cos θ = 14
= (2√3sin3θcosθ)
when cosθ=14=45√58
△2=△min occurs at cos θ = 12
= (2√3sin3θcosθ)
when cosθ=12=92
∴ 8√5△1−8△2=45−36=9