Answer:
Option B,C
Explanation:
Concept involved
This question is based on the concept of transcendal equation and sholud be solved with the help of graph
f(x)= x sin $\pi$ x, x>0
$f'(x)= sin\pi x+\pi xcos \pi x=0$
$\Rightarrow$ $ tan \pi x=-\pi x$
let f(x) = tan $\pi$ x and g(x)= - $\pi$ x
which could be plotted as,
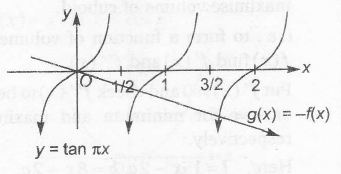
clearly , f(x) and g(x) intersect when
$\frac{1}{2}< x<1$
or $\frac{3}{2}< x<2$
or $\frac{5}{2}< x<3$
$\therefore$ a unique point in $(n+\frac{1}{2},n+1)$
or (n,n+1)