Discussion Forum

 The number of points in (-$\infty$, $\infty$) . for  which   $x^{2}-x\sin x-\cos x=0$ is

Answer:

Explanation:

Concept involved

 The given equation contains algebraic  and trigonometric function called transcendal equation . To solve transcendal  equations we should  always plot the graph for LHS  and RHS

Here,   $x^{2}=x\sin x+\cos x$

Let f(x)= x²  and   g(x) = x sin x+cos x

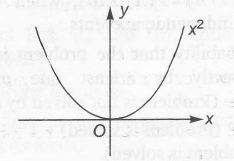
 we know the graph for f(x)= x²

 To plot , g(x) = x sinx+cos x

 g'(x) = x cos x+sinx-sinx 

            g'(x)= x cos x   .....(i)

 g"(x) =- x sinx +cos x  ......(ii)

 put  g'(x)=0

    $\Rightarrow $    x cos x=0

 $\therefore$         $x=0,\frac{\pi}{2},\frac{3\pi}{2},\frac{5\pi}{2},\frac{7\pi}{2},....$

at x=0,  $\frac{3\pi}{2},\frac{7\pi}{2}$,....f"(x) >0

 $\therefore$ minimum

   at x= $\frac{\pi}{2},\frac{5\pi}{2},\frac{9\pi}{2}$,.... f"(x)<0

minimum

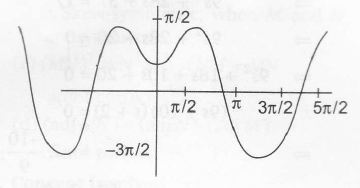
  $\therefore$    f(x) and g(x) are shown as

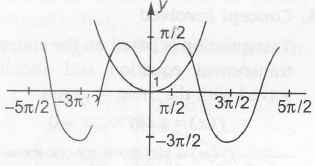
 $\therefore$   Number of solutions are 2.