Answer:
Option B
Explanation:
Concept involved
T o find the bounded area between y=f(x) and y= g(x) between x=a to x= b
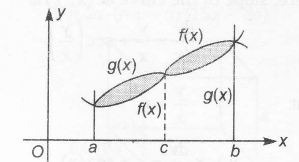
$\therefore$ Area bounded
$=\int_{a}^{c} [g(x) -f(x)]dx+\int_{c}^{b} [f(x)-g(x)]dx$
$\Rightarrow \int_{a}^{b} |f(x)-g(x)| dx$
Here , f(x)=y=sinx+cos x , when
$0\leq x \leq\frac{\pi}{2}$
and g(x) = y=|cos x-sinx |
$=\begin{cases}\cos x- \sin x, & 0\leq x\leq\frac{\pi}{4} \\\sin x-\cos x, & \frac{\pi}{4}\leq x \leq \frac{\pi}{2}\end{cases}$
Could be shown as
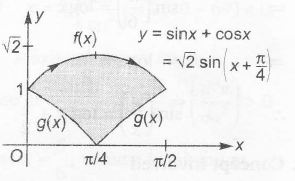
$\therefore$ Area bounded
$=\int_{0}^{\frac{\pi}{4}} \left\{(sinx+cos x)-(cos x-sinx)\right\} dx$
$+\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} \left\{(sinx+cos x)-(sin x-cosx)\right\} dx$
$=\int_{0}^{\frac{\pi}{4}} 2 sin x dx+\int_{\frac{\pi}{4}}^{\frac{\pi}{2}} 2cos x dx$
$=-2(cos x)^{\frac{\pi}{4}}_{0}+2(sin x.n)^{\frac{\pi}{2}}_{\frac{\pi}{4}}$
$=4-2\sqrt{2}=2\sqrt{2}(\sqrt{2}-1)$