Discussion Forum

1)

Let   $PR=3\hat{i}+\hat{j}-2\hat{k}$   and  $SQ=\hat{i}-3\hat{j}-4\hat{k}$ determine diagonals of a parallelogram PQRS and

 $PT=\hat{i}+2\hat{j}+3\hat{k}$   be another vector . Then, the volume  of the parallelopiped determined by the vectors PT,PQ and PS is

Answer:

Option C

Explanation:

 Concept involved . it involves law of   parallelogram and volume of parallelopiped . i.e,

 a+b=p  and b-a =q

              $a=\frac{p-q}{2}$

 and $b=\frac{p+q}{2}$

  

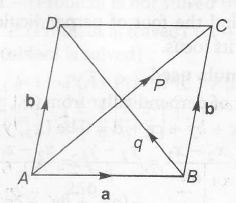
i.e, if p and q are diagonals of parallelograms , then its sides are $\frac{p-q}{2}$  and $\frac{p+q}{2}$

Situation analysis

 After finding the sides of parallelogram we should find volume of parallelopiped i.e, [a,b]

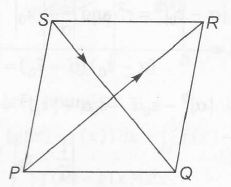
 HERE, sides of parallelogram are PQ and PS

 where,  $PQ=\frac{PR+SQ}{2}$

  =$PQ=\frac{(3\hat{i}+\hat{j}-2\hat{k})+(\hat{i}-3\hat{j}-4\hat{k})}{2}$

$PQ=2\hat{i}-\hat{j}-3\hat{k}$

 and PS=$\frac{PR-SQ}{2}$

   = $PS=\frac{(3\hat{i}+\hat{j}-2\hat{k})-(\hat{i}-3\hat{j}-4\hat{k})}{2}$

 PS =$\hat{i}+2\hat{j}+\hat{k}$

 $\therefore$     Volume of parallelopiped

  =[PT PQ PS]

 =  $\begin{bmatrix}1 & 2 &3\\2 & -1&-3\\1&2&1 \end{bmatrix}$

  =1(-1+6)-2(2+3)+3(4+1)

   =5-10+15=10