Discussion Forum

A particle of mass M and positive charge Q, moving with a  constant velocity   $u_{1}=4\hat{i}ms^{-1}$, enters a region of uniform static magnetic field normal to the x-y plane. The region of the magnetic field extends from x=0 to x=L for all values of y. After passing through this region , the particle emerges on the other side after 10 milliseconds with  a velocity   $u_{2}=2(\sqrt{3}\hat{i}+\hat{j})ms^{-1}$. The correct statement(s) is (are)

Answer:

Explanation:

 u= 4 $\hat{i}$ : v  $=2(\sqrt{3}\hat{i}+\hat{j})$ 

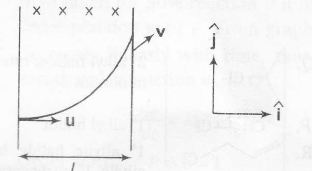
According  to the figure , magnetic field should be in $\otimes$ direction , or along -z direction

 Further ,   $\tan\theta =\frac{v_{y}}{v_{x}}=\frac{2}{2\sqrt{3}}=\frac{1}{\sqrt{3}}$

   $\therefore$     $\theta =30^{0} or\frac{\pi}{6}$

 = angle  of v with x-axis

 = angle rotated by the particle

  =Wt $=\left(\frac{BQ}{M}\right)t$

  $\therefore$      $B=\frac{\pi M}{6Qt}$

                             $=\frac{50\pi M}{Q}$   units   9as t =10^-3  second)