Answer:
Option A
Explanation:
From the momentum conservation equation, we have
Pi=Pj
∴m(u0cosα)ˆi+m(√u20−2gH)ˆj=(2m)v .......(i)
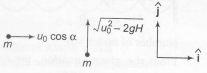
H=u20sin2α2g ........(ii)
From Eqs.(i) and (ii)
v=u0cosα2ˆi+u0cosα2ˆj
Since both components of v are equal. Therefore it is making 45° with horizontal.