Discussion Forum



1)

 If $f(x)= \int_{0}^{x} e^{t^{2}}(t-2)(t-3) dt,\forall x \epsilon (0,\infty),then$


A) f has a local maximum at x=2

B) f is decreasing on (2,3)

C) there exist some $ c \epsilon(0,\infty) $such that $f^{"}(c)=0$

D) f has a local minimum at x=3

Answer:

Option A,B,C,D

Explanation:

 Concept  involved

 use of Newton Leibnitz formula

 $\frac{d}{dx}\left\{\int_{f(x)}^{g(x)} \phi (t) dt\right\}=\phi(g(x)).g'(x)-\phi (f(x)).f'(x)$

 Sol. Here, $f(x) =\int_{0}^{x} e^{t^{2}} (t-2)(t-3) dt$

 $\Rightarrow$ $f'(x)=e^{x^{2}} (x-2)(x-3)$

18112021805_k1.PNG

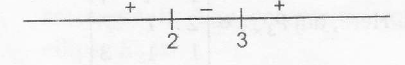
$\therefore$  maximum at x=2

 minimum at x=3

 decreasing on (2,3) 

 Also, f'(x)=0 has two roots x=2  and x=3

 i.e, $f'(2)=f'(3)=0$

 Thus, by rolle's theorm

 $f"(c)=0 $ must have atleast one root $\epsilon (2,3)$