Discussion Forum

1)

A tangent PT is drawn to the circle $x^{2}+y^{2}=4$ at the point $P(\sqrt{3},1)$ . a straight line L perpendicular to PT is a tangent to the circle $(x-3)^{2}+y^{2}=1$

A common tangent of the two circles is 

Answer:

Option D

Explanation:

(i) Equation of a tangent to at (x₁,y₁) is 

x²+y²=r²

 

at (x₁,y₁) is 

xx₁+yy₁=r²

(ii)If ax+by+c =0 is tangent to (x-h)²+(y-k)²=r²

|cp|=r

Here, equation of common tangnet be 

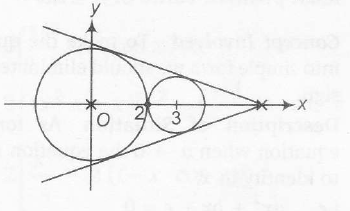
 $y=mx \pm 2\sqrt{1+m^{2}}$

 which is also the tangent to

  $(x-3)^{2}+y^{2}=1$

 $\Rightarrow$   $\frac{|3m-0+2\sqrt{1+m^{2}}|}{\sqrt{m^{2}+1}}=1$

 $\Rightarrow$   $3m+2\sqrt{1+m^{2}}=\pm \sqrt{1+m^{2}}$

 $\Rightarrow$  $3m=-3 \sqrt{1+m^{2}}$

or   $3m=-\sqrt{1+M^{2}}$

 $\Rightarrow$  $m^{2}=1+m^{2}$

or     $9m^{2}=1+m^{2}$

 $\Rightarrow$   $m \epsilon \phi$   or  $m=\pm \frac{1}{2 \sqrt{2}}$

$\therefore$    $y=\pm \frac{1}{2 \sqrt{2}} x \pm 2\sqrt{1+\frac{1}{8}}$

 $\Rightarrow$   $y=\pm \frac{x}{2 \sqrt{2}}\pm \frac{6}{2\sqrt{2}}$

 $\Rightarrow$  $2 \sqrt{2} y= \pm (x+6)$