Discussion Forum

1)

Let $a_{n}$ denote the number of all n-digit positive integers formed by the digits 0, 1 or both such that no consecutive digits, in them are 0. Let $b_{n}$ = The number of such n-digit integers ending with digit 1 and $c_{n}$ = The number of such n-digit integers ending with digit 0.

The value of $b_{6}$ is 

Answer:

Option B

Explanation:

Since $a_{n}$ be the n-digit positive integer formed by the digits 0,1 or both such that no two consecutive digits are zero.

 $b_{n}$=numbers which are ending with 1

$C_{n}$= number which are ending with 0

$\therefore$  $a_{n}=b_{n}+c_{n}$

 i.e, $a_{n}$=1(0 or 1)...............(0 or 1)

$b_{n}=$1 (0 or 1) ........1   

                                            nth place

 $c_{n}$=1(0 or 1) ......0

$b_{6}$= Six digit number ending with 1

 

Now, the four places are to be filled  

i,e,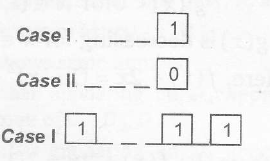

 For 3 places, all 1's are used =1 way

 one zero is used= $^{3}C_{1}$=3

 two zeros are used=1 way

 0  1  0  1  ............

 Total=5 ways

 

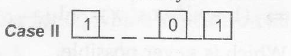
  for 3 places,

   all 1's are used =1ways

  one zero is used = $^{2}C_{1}$=2 ways

                                          ---------------------

                                               =3 ways

                                          ------------------

 Thus, $b_{6}=5+3=8$