Answer:
Option C
Explanation:
Concept involved if △ABC has sides a, b, c then,
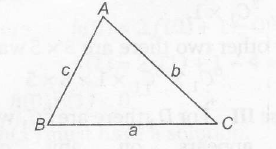
tan(A/2)=√(s−b)(s−c)a(s−a)
where, s=a+b+c2
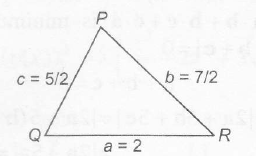
Sol ,s=2+72+522=4
∴ 2sinP−sin2P2sinP+sin2p=2sinP(1−cosP)2sinP(1+cosP)
=2sin2(P/2)2cos2(P/2)=tan2(P/2)
⇒ (s−b)(s−c)s(s−a)×(s−b)(s−c)(s−b)(s−c)
⇒ ((s−b)(s−c)2)△2=(4+72)2(4−52)2△2
=(34△)2