Discussion Forum



1)

 The ellipse   $E_{1}:\frac{x^{2}}{9}+\frac{y^{2}}{4}=1$ is  inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4)circumscribes the rectangle R. The eccentricity of the ellipse $E_{2}$ is 


A) $\frac{\sqrt{2}}{2}$

B) $\frac{\sqrt{3}}{2}$

C) $\frac{1}{2}$

D) $\frac{3}{4}$

Answer:

Option C

Explanation:

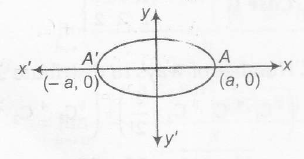
Concept involved equation of an ellipse is

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$    (a >b)

 Ecentricity  $e^{2}=1-\frac{b^{2}}{a^{2}}$       (a >b)

 2411202139_l2.PNG

 

 

Description of Situation As ellipse circumscribes the rectangle, then it must
pass through all four vertices.

Sol. Let the equation of Ellipse  $E_{2}$ be 

 $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ , where a<b and b=4

 24112021113_l3.PNG

 

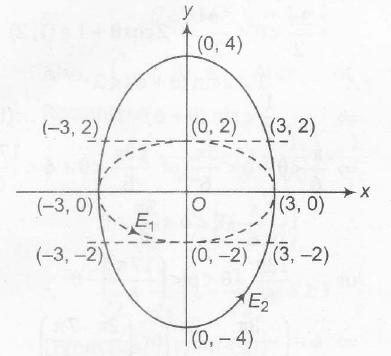
 Also, it passes through (3,2) 

 $\Rightarrow$   $\frac{9}{a^{2}}+\frac{4}{b^{2}}=1$                     $(\because$ b=4)

 $\Rightarrow$  $\frac{9}{a^{2}}+\frac{1}{4}=1 $ or  $a^{2}=12$

 Eccentricity of $E_{2}$

 $\Rightarrow$   $e^{2}=1-\frac{a^{2}}{b^{2}}=1-\frac{12}{16}=\frac{1}{4}$     $( \because $ a <b)

 $\therefore$  e=$\frac{1}{2}$