Discussion Forum

The locus of the end point of the chord of contact of tangents drawn from points lying on the straight line 4x-5y=20 to the circle $x^{2}+y^{2}=9$ is 

Answer:

Explanation:

Concept Involved if 

 $S: ax^{2}+2hxy+by^{2}+2gx+2fy+c$

then equation of chord bisected at P (x₁,y₁) is T=S₁

 or $axx_{1}+h(xy_{1}+yx_{1})+byy_{1}+g(x+x_{1})+f(y+y_{1})+C$

       =$ax_{1}^{2}+2hx_{1}y_{1}+by_{1}^{2}+2gx_{1}+2fy_{1}+C$

Description of Situation As equation of
chord of contact is T= 0

Sol. Here, equation of chord of contact wrt  P is 

$x\lambda+y\left(\frac{4\lambda-20}{5}\right)=9$

 $5 \lambda x+(4 \lambda-20)y=45$  .........(i)

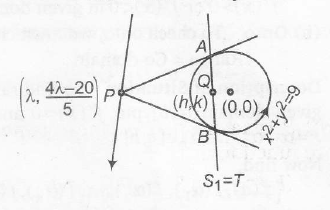
and equation of chord bisected at the point Q (h, k) is

 $xh+yk-9=h^{2}+k^{2}-9$

$\Rightarrow$  $xh+ky=h^{2}+k^{2}$.....(ii)

From Eqs.(i) and (ii)   We get

 $\frac{5 \lambda}{h}=\frac{4 \lambda-20}{k}=\frac{45}{h^{2}+k^{2}}$

$\therefore$  $\lambda=\frac{20h}{4h-5k}$ and   $\lambda=\frac{9h}{h^{2}+k^{2}}$

$\Rightarrow$   $\frac{20h}{4h-5k}=\frac{9h}{h^{2}+k^{2}}$

 or   $20(h^{2}+k^{2})=9(4h-5k)$

or     $20(x^{2}+y^{2})=36x-45y$