Discussion Forum

In the given circuit, the AC source has $\omega$ = 100 rad/s. Considering the inductor and capacitor to be ideal, the correct choice(s) is(are)

Answer:

Explanation:

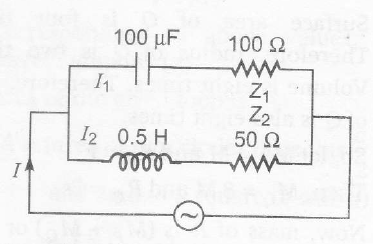
Circuit I

  $X_{C}=\frac{1}{\omega C}=100 \Omega$

 $\therefore$ 

 $z_{1}=\sqrt{(100)^{2}+(100)^{2}}=100\sqrt{2} \Omega$

 $\phi_{1}=\cos^{-1}\left(\frac{R_{1}}{Z_{1}}\right)=45^{0}$

In this circuit current leads the voltage 

 $I_{1}=\frac{V}{Z_{1}}=\frac{20}{100 \sqrt{2}}=\frac{1}{5 \sqrt{2}}A$

$V_{100 \Omega}= (100) I_{1}=(100) \frac{1}{5 \sqrt{2}}V$

  $=10\sqrt{2}$V

 Circuit 2

  $X_{L}=\omega L=(100)(0.5)=50 \Omega$

 $Z_{2}=\sqrt{(50)^{2}+(50)^{2}}=50\sqrt{2}\Omega$

$\phi_{2}=\cos^{-1}\left(\frac{R_{2}}{Z_{2}}\right)=45^{0}$

in this circuit voltage leads the current

 $I_{2}=\frac{V}{Z_{2}}=\frac{20}{50\sqrt{2}}=\frac{\sqrt{2}}{5}$ A

$V_{50\Omega}=(50)I_{2}=50\left(\frac{\sqrt{2}}{5}\right)=10\sqrt{2}V$

Further $I_{1}$ and $I_{2}$ have a mutual phase  difference of  $90^{0}$

$\therefore$      $I=\sqrt{I_{1}^{2}+I_{2}^{2}}=\sqrt{\frac{1}{50}+\frac{4}{50}}=\frac{1}{\sqrt{10}}$

   =0.3 A