Discussion Forum

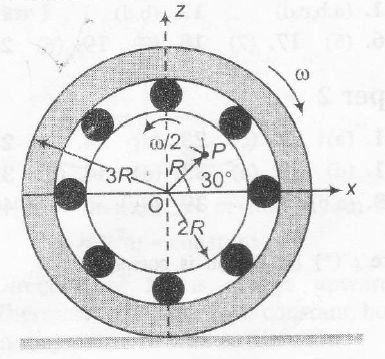
The figure shows a system consisting of (i) a ring of outer radius 3R rolling clockwise without slipping on a horizontal surface with angular speed $\omega$ and (ii) an inner disc of radius 2R rotating anti-clockwise with angular speed $\omega/2$. The ring and disc are separated by frictionless ball bearings. The system is in the x-z plane. The point P on the inner disc is at a
distance R from the origin, where OP  makes an angle of $30^{0}$ with the horizontal. Then with respect to the horizontal surface.

Answer:

Explanation:

 Velocity of point O is 

  $v_{0}=(3R\omega)\widehat{i}$

 $V_{PO}$ is $\frac{R.\omega}{2}$ in the direction shown in the figure. In vector form

 $v_{PO}=-\frac{R \omega}{2} \sin 30^{0}\widehat{i}+\frac{R\omega}{2}\cos 30^{0} \widehat{k}=-\frac{R\omega}{4}\widehat{i}+\frac{\sqrt{3}R\omega}{4}\widehat{i}$

 bu  $v_{PO}=v_{P}-v_{O}$

$\therefore$  $v_{p}=v_{po}+v_{o}$

 $=\left(-\frac{R\omega}{4}\widehat{i}+\frac{\sqrt{3}R\omega}{4}\widehat{k}\right)+3R \omega \widehat{i}$

 $=\frac{11}{4} R\omega \widehat{i}+\frac{\sqrt{3}}{4}R \omega \widehat{k}$