Discussion Forum

A lamina is made by removing a small disc of diameter 2.R from a bigger disc of uniform-rnass densiry and radius 2R, as shown in the figure.The moment of inertia of this lamina about axes passing through O and P is $I_{0}$ and $I_{p}$ respectively'.Both these axes are perpendicular to the plane  of the lamina. The ratio $\frac{I_{p}}{I_{0}}$ to the nearest  integer is 

Answer:

Explanation:

T= total portion

R= Remaining portion and

 C= cavity and

let $\sigma=$ mass per unit area

 then, $m_{T}=\pi (2R)^{2} \sigma=4 \pi R^{2} \sigma$

  $m_{C}=\pi (R)^{2} \sigma=\pi r^{2} \sigma$

For $I_{P}$

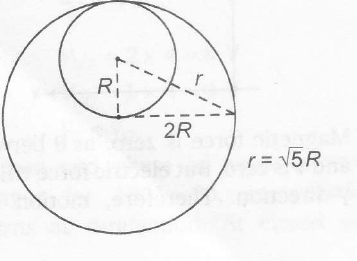
$I_{R}=I_{T}-I_{C}$

=$\frac{3}{2}m_{T}(2R)^{2}-\left[\frac{1}{2} m_{C}R^{2}+m_{C}r^{2}\right]$

 =$\frac{3}{2}(4\pi R^{2} \sigma)(4R^{2})-\left[\frac{1}{2}(\pi R^{2} \sigma)+(\pi R^{2} \sigma)(5R^{2})\right]$

=($18.5 \pi R^{4} \sigma)$

For $I_{0}$

=$\frac{1}{2}m_{T}(2R)^{2}-\frac{3}{2}m_{C}R^{2}$

  =$\frac{1}{2}(4 \pi R^{2}\sigma)(4R^{2})-\frac{3}{2}(\pi R^{2} \sigma)(R^{2})$

=$6.5  \pi R^{4} \sigma$

$\therefore$  $\frac{I_{P}}{I_{Q}}=\frac{18.5 \pi R^{4} \sigma}{6.5 \pi R^{4} \sigma}=2.846$

Therefore, the nearest integer is 3.