Discussion Forum

A small mass m is attached to a massless string whose other end is fixed at P as shown in the figure. The mass is undergoing circular motion in the x-y plane with centre at O  and constant angular speed $\omega$.If the angular momentum  of the system, calculated  about O and P  are denoted  by $L_{o}$ and $L_{p}$ respectively, then 

Answer:

Explanation:

Angular momentum of a particle about a
point is given by :

$L = r \times p =m (r \times v)$

 For $L_{0}$

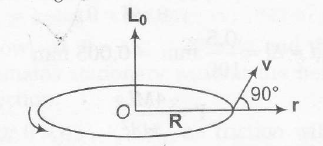
|L|=$(mvr \sin \theta)=m(R \omega)(R) \sin 90^{0}$

 =$mR^{2} \omega$= constant 

Direction of $L_{0}$ is always upwards , Therefore  , complete $L_{0}$  is constant , both  in magnitude as well as direction

For $L_{p}$

$|L_{p}|=(mvr \sin \theta)$

                     =$(m)(R\omega)(l) \sin90^{0}$

  =$(mRl \omega)$

magnitude  of $L_{p}$ will remain constant but  direction of $L_{p}$ keeps on changing