Discussion Forum

Let E and F be two independent events. The probability that exactly one of them occurs is 11/25 and the probability of none of them occurring is 2/25.lf P(T) denotes the probability of occurrence of the event T, then

Answer:

Explanation:

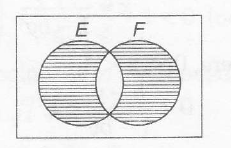
  $P( E \cup F)-P(E \cap F)=\frac{11}{25}$.....(i)

 (i.e, only E or only F)

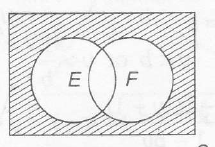
 Neither of them occurs =$\frac{2}{25}$

 $\Rightarrow$    $P(\overline{E} \cap \overline{F})=\frac{2}{25}$......(ii)

 From . Eq.(i), we get

 $P(E)+P(F)-2P(E \cap F)=\frac{11}{25}$ ...(iiI)

 From . Eq.(ii), we get

 $(1-P(E))(1-P(F))=\frac{2}{25}$

$\Rightarrow$  $1-P(E)-P(F)+P(E).P(F)=\frac{2}{25}$.....(iv)

 From eqs.(iii)  and (iv) , we get

 $P(E)+P(F)=\frac{7}{5}$  $P(E).P(F)=\frac{12}{25}$

 $\therefore$  $P(E) .\left\{ \frac{7}{5}-P(E)\right\}=\frac{12}{25}$

$\Rightarrow$   $(P(E))^{2}-\frac{7}{5} P(E)+\frac{12}{25}=0$

 $\Rightarrow$  $\left(P(E)-\frac{3}{5}\right)\left(P(E)-\frac{4}{5}\right)=0$

 $\therefore$    $P(E)= \frac{3}{4}$ or $\frac{4}{5}$  $\Rightarrow  P(F)= \frac{4}{5}$ or $\frac{3}{5}$