Discussion Forum

1)

Let $f(\theta)=\sin\left[ \tan^{-1}\left(\frac{\sin \theta}{\sqrt{\cos 2 \theta}}\right)\right]$  where  

$-\frac{\pi}{4}< \theta < \frac{\pi}{4}$ .Then. the value of $\frac{d}{d(\tan \theta)} (f(\theta))$ is 

Answer:

Option D

Explanation:

 $f(\theta)= \sin\left(\tan^{-1}\frac{\sin \theta}{\sqrt{\cos 2 \theta}}\right)-\frac{\pi}{4}< \theta <\frac{\pi}{4}$

 Let $\tan^{-1} \frac{\sin \theta}{\sqrt{\cos 2 \theta}d}=\phi$

 $\Rightarrow$   $\tan \phi = \frac{\sin \theta}{\sqrt{\cos 2 \theta}}$

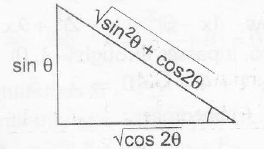
 $\therefore$   $\sin \phi=\frac{\sin \theta}{\sqrt{ \sin^{2} \theta+\cos 2 \theta}}$

 =$\frac{\sin \theta}{\sqrt{1-\sin^{2} \theta}}= \frac{\sin \theta}{\cos \theta}=\tan \theta$

$\therefore$   $f(\theta)= \sin \phi=\tan \theta$

 $\Rightarrow$   $\frac{d f(\theta)}{d( \tan \theta)}=1$