Discussion Forum

Let U₁ and U₂ be two urns such that U₁ contains 3 white and 2 red balls and U₂ contains only 1 white ball. A fair coin is tossed. If head appears then 1 ball is drawn at random from U₁ and put into U₂. However, if tail appears then 2 balls are drawn at random from U₁ and put into U₂. Now, 1 ball is drawn at random from U₂

The probability of the drawn ball from U₂ being  white is

Answer:

Explanation:

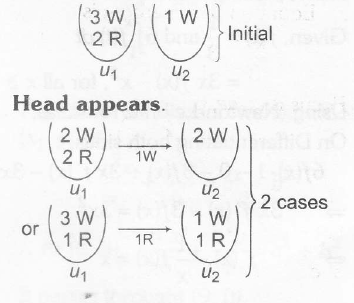
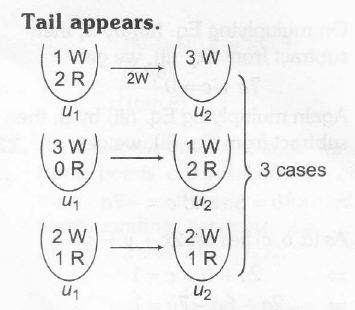
Now , probability of the drawn ball from $U_{2}$ being  white is 

 $\Rightarrow$ P( white /U₂)

 =  $P(H).\left\{\frac{^{3}C_{1}}{^{5}C_{1}}\times\frac{^{2}C_{1}}{^{2}C_{1}}+\frac{^{2}C_{1}}{^{5}C_{1}}\times\frac{^{1}C_{1}}{^{2}C_{1} }\right\}$ $+ P(T)\left\{\frac{^{3}C_{1}}{^{5}C_{1}}\times\frac{^{3}C_{2}}{^{3}C_{2}}+\frac{^{2}C_{2}}{^{5}C_{2}}\times\frac{^{1}C_{1}}{^{3}C_{2}}$

$+\frac{^{3}C_{1}.^{2}C_{1}}{^{5}C_{2}}\times\frac{^{2}C_{1}}{^{3}C_{2}}\right\}$

Now ,P(white/U₂)=$\frac{1}{2}\left\{\frac{3}{5}\times1+\frac{2}{5}\times\frac{1}{2}\right\}$

$+\frac{1}{2}\left\{\frac{3}{10}\times1+\frac{1}{10}\times\frac{1}{3}+\frac{6}{10}\times\frac{2}{3}\right\}=\frac{23}{30}$