Discussion Forum



1)

Column I shows four systems, each of the same length L, for producing standing waves. The lowest possible natural frequency of a system is called its fundamental frequency, whose wavelength is denoted as $\lambda_{f}$ . Match each system with statements given in Column II describing the nature and wavelength of the standing waves.

29112021837_ty.PNG


A) (A) $\rightarrow$ (p,t), (B) $\rightarrow$ (p,s),(C) $\rightarrow$ (q,s),(D) $\rightarrow$ (q,r)

B) (A) $\rightarrow$ (p,s), (B) $\rightarrow$ (p,t),(C) $\rightarrow$ (q,s),(D) $\rightarrow$ (q,r)

C) (A) $\rightarrow$ (p,s), (B) $\rightarrow$ (p,s),(C) $\rightarrow$ (q,s),(D) $\rightarrow$ (p,t)

D) (A) $\rightarrow$ (q,t), (B) $\rightarrow$ (p,s),(C) $\rightarrow$ (q,t),(D) $\rightarrow$ (q,r)

Answer:

Option A

Explanation:

In organ pipes, longitudinal waves are formed. In string, transverse waves are formed. Open-end of pipe is displacement antinode and closed end is the displacement node. In case of string fixed end of a string is node.

Further, least distance between a node and an antinode is  $\frac{\lambda}{4}$ and between two  nodes is $\frac{\lambda}{2}$  Keeping these Points in mind answer to this question is as under

 (A) $\rightarrow$  (p,t)

(B) $\rightarrow$  (p,s)

(C) $\rightarrow$  (q,s)

(D) $\rightarrow$  (q,r)

Analysis of Question
(i) Unlike the Previous years few match the column Problems, this question seems to be more logical' If you know the subject, You can select
correct matching without confusion.
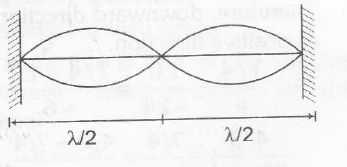
(ii) In option (d) of column I, the string is fixed from centre, therefore at lowest frequency, two loops will be formed as shown below

30112021109_g1.PNG