Discussion Forum

1)

Water (with refractive index =$\frac{4}{3}$) in a tank is 18 cm deep. Oil of refractive index  $\frac{7}{4}$  lies on the water making a convex surface of radius of curvature R = 6 cm as shown. Consider oil to act as a thin lens. An object S is placed 24 cm above the water surface. The location of its image is at x cm above the bottom of the tank. Then, x is

Answer:

Option B

Explanation:

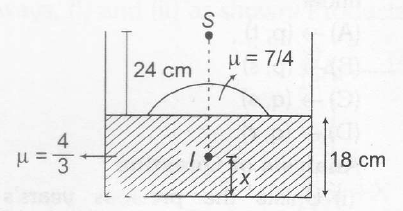
 Two refractions will take place, first from the spherical surface and the other from the plane surface. So, applying 

   $\frac{\mu_{2}}{v}-\frac{\mu_{1}}{u}= \frac{ \mu_{2}-\mu_{1}}{R}$

two times with proper sign convention. Ray of light is travelling downwards.
Therefore, downward direction is taken as positive direction.

$\frac{7/4}{v}-\frac{1.0}{-24}= \frac{ 7/4-1.0}{+6}$.....(i)

$\frac{4/3}{(18-x)}-\frac{7/4}{v}= \frac{ 4/3-7/4}{\propto}$

Solving these equations, we get 

                  x=2 cm

$\therefore$   Answer is 2