Discussion Forum

A thin ring of mass 2 kg and radius 0.5 m is rolling without slipping on a horizontal plane with  velocity 1 m/s. A small ball of mass 0.1 kg, moving with velocity 20 mls in the opposite directions, hits the ring at a height of 0.75 m and goes vertically up with velocity 10m/s imrnediately after the collision

Answer:

Explanation:

The data is incomplete. Let us assume that friction from ground on ring is not
impulsive during impact.
From linear momentum conservation in horizontal direction, we have

$(2 \times 1)+(0.1 \times 20)= (0.1 \times 0)+(2 \times v) \leftarrow^{-v}\rightarrow^{+ve}$

 Here, v is the ve;locity of CM of ring after impact 

Solving the above equation, we have
                            u=0
Thus, CM becomes stationary.

$\therefore$ correct answer is (a)

Linear impulse during impact
(i) In horizontal direction

 $J_{1}=\triangle P=0.1 \times v20=2Ns$

 (ii) In vertical direction

 $J_{2}=\triangle P = 0.1 \times 10 =1 Ns$

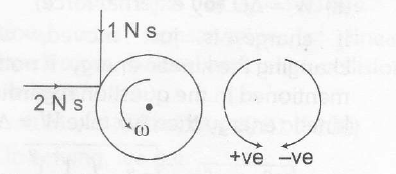
 Writing the equation (about CM) 

Angular impulse= change in angular momentum

    $1\times\left(\frac{\sqrt{3}}{2}\times\frac{1}{2}\right)-2\times0.5\times\frac{1}{2}$

  $=2\times(0.5)^{2}\left[ \omega-\frac{1}{0.5}\right]$

Solving this equation ω comes out to be positive or ω anti-clockwise. So just after collision rightwards slipping is taking place.
Hence, friction is leftwards.
Therefore, option (c) is also correct

Correct options are (a) and (c).