Discussion Forum



1)

Two solid spheres A and B of equal volumes but of different densities dA and dB are connected by a string. They are fully immersed in a fluid of density dF. They get arranged into an equilibrium state as shown in the figure with a tension in the string. The arrangement is possible only if

29112021540_f5.PNG


A) $d_{A}$ < $d_{F}$

B) $d_{B}$ > $d_{F}$

C) $d_{A}$ > $d_{F}$

D) $d_{A}$ +$d_{B}$ =2 $d_{F}$

Answer:

Option A,B,D

Explanation:

30112021366_t2.PNG

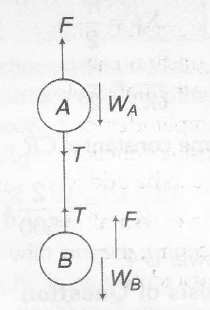
  F= Upthrust=  $V d_{F} g$

Equilibrium of A

 $V d_{F} g= T+W_{A}$

                   =$ T+V d_{A} g$

 Equilibrium of B

  $T+Vd_{F} g=Vd_{B} g$

Adding Eqs. (i) and (ii), we get

 $2d_{F}=d_{A}+d_{B}$

 $\therefore$ Option(d) is correct

From Eq. (i), we can see that

  $d_{F}  >d_{A}$       [as T >0]

$\therefore$ Option (a) is correct

From Eq. (ii) we can see that

 $d_{B} >d_{F}$

$\therefore$ Option (a) is correct.

$\therefore$ Correct options are (a), (b) and (d)