Discussion Forum

Four-point charges, each of +q are rigidly fixed at the four corners of a square planar soap film of side a. The surface tension, of the soap film is $\gamma$ . The system of charges and planar film are in equilibrium and, $a =k\left[\frac{q^{2}}{\gamma}\right]^{1/N}$. where k is a constant. Then N is 

Answer:

Explanation:

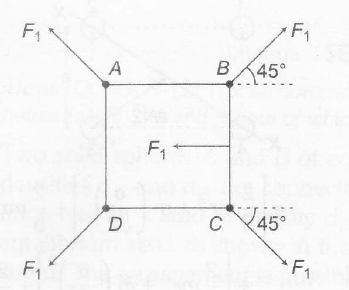
$F_{1}=$ Net electrostatic force on anyone charge due to rest of three charges

   =$\frac{1}{4 \pi \epsilon_{0}}\frac{q^{2}}{a^{2}}(\sqrt{2}+\frac{1}{2})$

 $F_{2}$= surface tension force =$\gamma a$

 If we see the equilibrium of line BC, 

then $2F_{1} \cos 45^{0}=F_{2}$

 or   $ \sqrt{2} F_{1}=F_{2}$

 or  $\frac{1}{4 \pi \epsilon_{0}}\frac{q^{2}}{a^{2}}(2+\frac{1}{\sqrt{2}})=\gamma a$

 $\therefore$ $a^{3}= \frac{1}{4 \pi \epsilon_{0}}(2+\frac{1}{\sqrt{2}})\frac{q^{2}}{\gamma} $

 or    $a= [\frac{1}{4 \pi \epsilon_{0}}(2+\frac{1}{\sqrt{2}})]^\frac{1}{3}[\frac{q^{2}}{\gamma}]^\frac{1}{3}$

   $=k\left[\frac{q^{2}}{\gamma}\right]^{1/3}$

 where  , $k=\left\{\frac{1}{4 \pi \epsilon_{0}}(2+\frac{1}{\sqrt{2}})\right\}^{1/3}$

 Therefore    ,N=3

 Answer is 3