Phase space diagrams are useful tools in analyzing all kinds of dynamic problems. They are espcially useful in studying the changes in motion as initial position and momenturn are
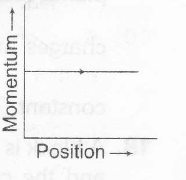
changed. Here we consider some simple dynamical systems in one dimension. For such sysfems, phase space is a plane in which position is plotted along horizontol axis and momentum is plotted along vertical axis. The phase space diagram is x(t) vs p(t) curue in this plane. The arrow on the curve indicates the time flow. For example, the phase space diagram for a particle moving with constant velocity is a straight line as shown in the figure. We use the sign convention in which position or momentum upwards (or to right) is positive and downwards (or to left) is negative
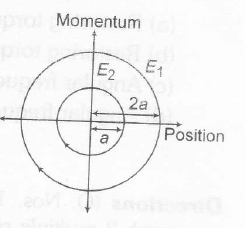
The phase space diagram for a simple harmonic motion is circle centerecl at the origin. In the figure , the two circles represent the same osciliator but for different initial conditions , and $E_{1}$ and $E_{2}$ are the total mechanical energies respectively , Then