Answer:
Option A
Explanation:
For hydrogen or hydrogen type atoms
$\frac{1}{\lambda}=RZ^{2}\left(\frac{1}{n_{f}^{2}}-\frac{1}{n_{i}^{2}}\right)$
In the transition from $n_{i} \rightarrow n_{f}$
$\therefore$ $\lambda \propto \frac{1}{Z^{2}\left(\frac{1}{n^{2}_{f}}-\frac{1}{n_{i}^{2}}\right)}$
$\therefore$ $\frac{\lambda_{2}}{\lambda_{1}}=\frac{Z_{1}^{2}\left(\frac{1}{n^{2}_{f}}-\frac{1}{n_{i}^{2}}\right)_{1}}{Z_{2}^{2}\left(\frac{1}{n^{2}_{f}}-\frac{1}{n_{i}^{2}}\right)_{2}}$
$\lambda_{2}=\frac{\lambda_{1}Z_{1}^{2}\left(\frac{1}{n^{2}_{f}}-\frac{1}{n_{i}^{2}}\right)_{1}}{Z_{2}^{2}\left(\frac{1}{n^{2}_{f}}-\frac{1}{n_{i}^{2}}\right)_{2}}$
Substituting the values , we have
$Å \frac{(6561 Å)(1)^{2}\left(\frac{1}{2^{2}}-\frac{1}{3^{2}}\right)}{(2)^{2}\left(\frac{1}{2^{2}}-\frac{1}{4^{2}}\right)}=1215$Å
$\therefore$ correct option is (a)
Analysis of Question
(i) Question is simple.
(ii) In modern physics, mostly questions are asked on the emission of a photon by the transition of electrons from some higher energy state to some lower energy state
(iii) For hydrogen and hydrogen-like atoms which have onlY single
electron, we can use the formula
$\frac{1}{\lambda}=RZ^{2}\left(\frac{1}{n_{f}^{2}}-\frac{1}{n^{2}_{i}}\right)$
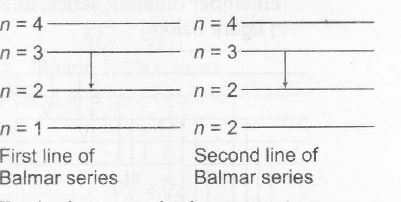
(iv) Further, the student should also remember different series, as shown
in figure below
