Discussion Forum

1)

A ball of mass (m)0.5 kg is attached to the end of a string having a length (L)0.5 m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball (in rad/s) is

Answer:

Option D

Explanation:

 

 

 

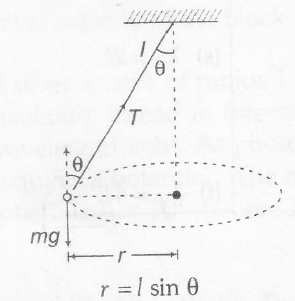
T $\cos \theta$ component will cancel mg

 $T \sin \theta$  component will provide necessary centripetal force to the ball towards  centre C

 $\therefore$   $ T \sin \theta =mr \omega^{2} = m(l \sin \theta) \omega^{2}$

 $\therefore$   $ \omega= \sqrt{\frac{T}{ml}}$

 or    $\omega_{max}=\sqrt{\frac{T_{max}}{ml}}=\sqrt{\frac{324}{0.5 \times 0.5}}$

 =36 rad/s

 $\therefore$   correct option is (d) 

 

Analysis of Question
(i) Question is simple

(ii) This is called the conical pendulum

(iii)The interesting fact in this problem is that ω or T is independent of  $\theta$

 $\omega \propto \sqrt{T}$

 If $\omega$  is increased, T will also increase